THIS CALCULATOR CAN SOLVE ALL OF ABOVE PROBLEMS AND MORE
Students can use this calculator to check homework solutions
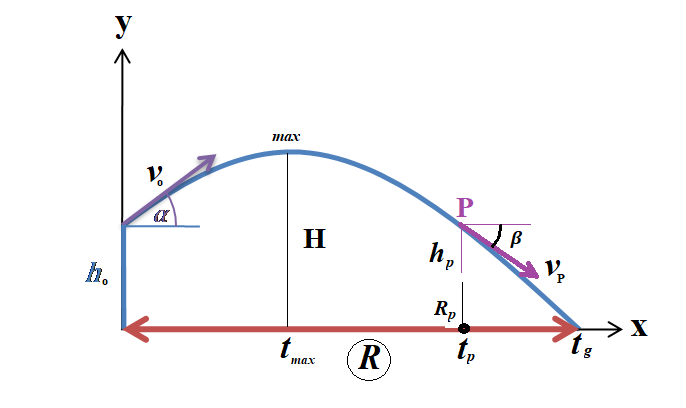
Look at the following picture to know the names of all variables
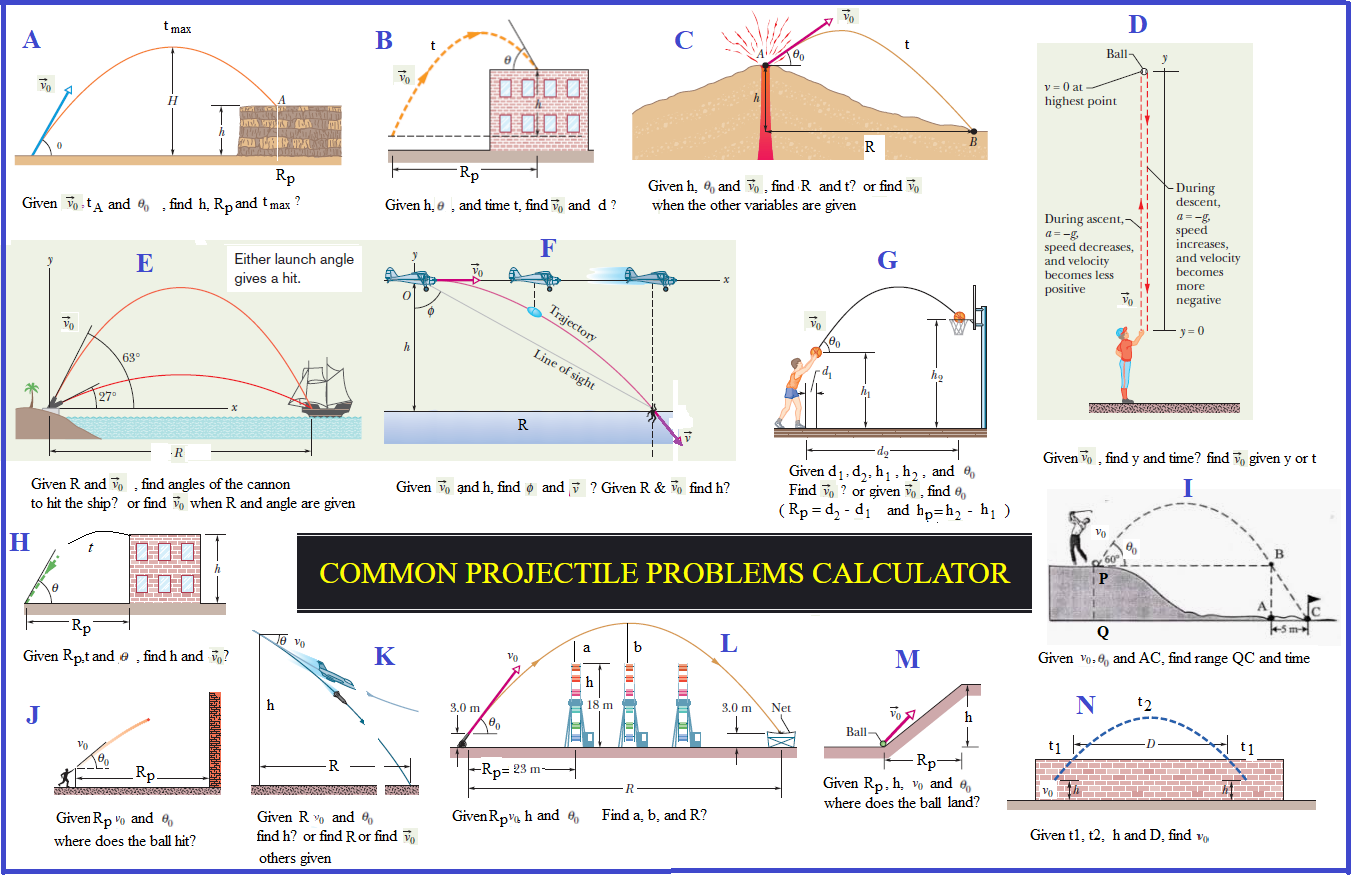
THIS CALCULATOR CAN SOLVE ALL OF ABOVE PROBLEMS AND MORE
Students can use this calculator to check homework solutions
Look at the following picture to know the names of all variables

The Projectile Trajectory
Darker trajectory means slower motion. Refresh the page every run.
SOME SAMPLE PROBLEMS AND INSTRUCTION:
Sample A:
A stone is projected at a cliff of height h with an initial speed of 42 m/s directed at angle 60 degrees above the horizontal. The stone strikes at point P, 5.5s after launching. Find the height h of the cliff? (Enter: Vo=42, alpha=60, tp=5.5 Find hp) The speed of the stone just before impact at P? (Find Vp) The maximum height H reached above the ground? (Find H)
Sample B:
In Fig. B, a ball is thrown up onto a roof, landing 4.00 s later at height h = 20.0 m above the release level. The ball’s path just before landing is angled at 60.0° with the roof. (a) Find the horizontal distance d it travels. What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s initial velocity? (We do the reverse problem: a ball is thrown from the roof with initial angle of 60.0 degrees and it hits the ground after 4 s. Enter: alpha=60, tg=4, ho=20. Find R, Vp and absolute value of angle beta)
Sample C:
During volcanic eruptions, chunks of solid rock can be blasted out of the volcano; these projectiles are called volcanic bombs. Figure C shows a cross section of Mt.Fuji, in Japan. (a) At what initial speed would a bomb have to be ejected, at angle 35° to the horizontal, from the vent at A in order to fall at the foot of the volcano at B, at vertical distance h = 3.30 km and horizontal distance d = 9.40 km? Ignore, for the moment, the effects of air on the bomb’s travel (Change km to meter first. Enter: alpha=35, ho=3300, R=9400 Find Vo) (b) What would be the time of flight? (Find tg)
Sample D:
A pitcher tosses a baseball up along a y axis, with an initial speed of 12 m/s. How long does the ball take to reach its maximum height? (Enter: Vo=12, alpha=90. Find tmax) What is the ball's maximum height above its release point (Find H)? How long does it take to take the ball to reach a point 5 m above its release point? (Enter: Vo=12, alpha=90, hp=5. Find tp)
Sample D:
A rock is dropped (from rest) from a top of 100 m tall buiding. How long does it take for the rock to hit ground? (Enter: ho=100, alpha=-90. Find tg). What is the speed of the rock just before it hits ground? (Find vg)
Sample E:
A man is fired from a cannon at an angle 30 degrees with initial velocity 25 m/s.How long does it take for the man to reach its highest point? (Enter: Vo=25, alpha=30. Find tmax). What is the maximum high the man can reach? (Find H) What horizontal distance does the man travel? (Find R)
Sample E:
A pirate ship is 560 m from a harbor entrance. A defense cannon, located at sea level on the harbor entrance, fires balls at initial speed Vo = 82 m/s. At what angle from the horizontal must a ball be fired to hit the ship? (Enter: Vo=82, R=560. Find alpha) What is maximum range of the cannonballs? (Enter: Vo=82, alpha=45. Find R)
Sample E:
A pirate ship is 600 m from a harbor entrance. A defense cannon, located at sea level on the harbor entrance, fires balls at an angle of 50 degrees. What is the speed of the cannon ball be fired to hit the ship? (Enter: alpha=50, R=600. Find Vo)
Sample F:
A rescue plane flies at 55.0 m/s and constant height h = 500 m toward a point directly over a victim, where a rescue capsule is to land. What should be the angle Ф of the pilot’s line of sight to the victim when the capsule release is made? (Enter: Vo=55, ho=500. Find R and then find arctan(R/h))
Sample G:
At what initial speed must the basketball player in Fig. G throw the ball, at angle 55° above the horizontal, to make the foul shot? The horizontal distances are d1 = 1.0 ft and d2 = 14 ft, and the heights are h1 = 7.0 ft and h2 = 10 ft. (Change ft to meter, then enter: alpha=55, Rp= d2-d1, hp= h2-h1. Look for Vo)
Sample H:
In Fig. H, a ball is thrown leftward from the left edge of the roof, at height h above the ground. The ball hits the ground 1.50 s later, at distance d = 25.0 m from the building and at angle 60.0° with the horizontal. (a) Find h? What are the (b) magnitude and (c) angle relative to the horizontal of the velocity at which the ball is thrown? (d) Is the angle above or below the horizontal? (We do a reverse problem: Shoot from ground to the top of the roof. Enter: alpha=60, tp=1.5, Rp=25. Look for hp, Vp and beta)
Sample I:
Look at fig. I, Enter Vo, alpha, we can find distance PB and R=QC=PB+AC. We can find tg=R/(Vo.cos(alpha)) or refresh browser and enter: Vo, alpha, and R to find tg and ho)
Sample J:
Look at fig. J, You throw a ball toward a wall at speed 25.0 m/s and at angle 40.0° above the horizontal. The wall is distance d = 22.0 m from the release point of the ball. (a) How far above the release point does the ball hit the wall? What are the (b) horizontal and (c) vertical components of its velocity as it hits the wall? (d) When it hits, has it passed the highest point on its trajectory? (Enter: Vo=25, alpha=40, Rp=22, look for hp, Vp and beta, then calculate horizontal and vertical components of its velocity by using vp and beta. For question d: Do another run, find tmax by entering only Vo and alpha. Compare tmax, and tp which you got in the first run. if tp > tmax, then the ball passed the highest point on its trajectory)
Sample K:
A certain airplane has speed of 290.0 km/h (80.6 m/s) and is diving at an angle of 30.0° below the horizontal when the pilot releases a radar decoy. The horizontal distance between the release point and the point where the decoy strikes the ground is d = 700 m. (a) How long is the decoy in the air? (b) How high was the release point? (Enter: Vo=80.6, alpha= -30, R=700, look for tg, ho)
Sample L:
Look at fig. L, enter Vo, alpha, and Rp. Find hp then compute (hp-15). For question (b) enter only Vo and alpha to find tmax and Hmax, then compute (Hmax-15). Because of symetry, answer of question (c) is the same as (a))
Sample M:
A ball is launched with a velocity of magnitude 10.0 m/s, at an angle of 50.0° to the horizontal. The launch point is at the base of a ramp of horizontal length d1 = 6.00 m and height d2 = 3.60 m. A plateau is located at the top of the ramp. Does the ball land on the ramp or the plateau? (Enter: Vo=10, alpha=50, Rp=d1=6. Find hp? if hp < d2 (d2=3.6), the ball lands on the ramp. Otherwise, it lands on the plateau.)
Sample N:
A baseball is hit at a height h = 1.00 m and then caught at the same height. It travels alongside a wall, moving up past the top of the wall 1.00 s after it is hit and then down past the top of the wall 4.00 s later, at distance D = 50.0 m farther along the wall. (a) What horizontal distance is traveled by the ball from hit to catch? What are the (b) magnitude and (c) angle (relative to the horizontal) of the ball’s velocity just after being hit? (d) How high is the wall? (Enter: R=D=50, tg=4. Find Vo, alpha. From Vo and alpha, compute V1y=VoSin(alpha). This is V1y at the top of the wall and we also know V1x = VoCos(alpha) = constant = Vox. By using formula V1y = Voy - gt where t=1s, we can calculate initial vertical velocity component Voy (at the hitting point).Thus we can compute Vo from Voy and Vox. Now we refresh browser and do another run: enter Vo and time tg = 1 + 4 + 1 = 6, we can get R, initial angle alpha and new Hmax = H + 1)
Sample E & J:
A batter hits a pitched ball when the center of the ball is 1.22 m above the ground. The ball leaves the bat at an angle of 45° with the ground.With that launch, the ball should have a horizontal range (returning to the launch level) of 107 m. (a) Does the ball clear a 7.32-m-high fence that is 97.5 m horizontally from the launch point? (b) At the fence, what is the distance between the fence top and the ball center? (Enter: alpha=45, R=107. Find Vo. Second run: enter Vo, ho=1.22, alpha=45 and Rp=97.5 Find hp. Compare hp and 7.32 m high fence to know the ball clear the fence or not and distance between the fence top and the ball center.)
Sample A & E:
In basketball, hang is an illusion in which a player seems to weaken the gravitational acceleration while in midair. The illusion depends much on a skilled player’s ability to rapidly shift the ball between hands during the flight, but it might also be supported by the longer horizontal distance the player travels in the upper part of the jump than in the lower part. If a player jumps with an initial speed of v0 = 7.00 m/s at an angle of 35.0°, what percent of the jump’s range does the player spend in the upper half of the jump (between maximum height and half maximum height)? (Enter: Vo=7, alpha=35. Find Hmax and tmax. Second run: enter Vo=7, alpha=35 and hp=Hmax/2, find tp. Then compute the percentage difference between tmax and tp.)